During manske, Cl- ions are added (typically using NaCl) to a harmalaH+ solution (typically from rue seed water extraction). The solution is cooled, and the presence of the common Cl- ion precipitates harmalaHCl. Remaining liquid is removed (along with unwanted plant material) and the precipitated harmalaHCl recovered.
For manske to work, both Cl- and harmalaH+ concentrations need to be chosen appropriately:
a) If Cl- concentration high, salt contamination will increase along with unwanted plant material (e.g. proteins) that could precipitate at high ionic strength.
b) If HarmalaH+ concentration is too high, there may not be enough water to remove unwanted plant material.
c) If either are too low, precipitation will be insufficient or not occur.
Following a good tek avoids these issues 🤞. For those interested in more details 🤓, we can look at the equilibrium equation as an approximation to the complex plant extract.
Definitions:
c: Molarity of shared chlorine in ions before precipitation.
h: Molarity of harmalas before precipitation.
s : Solubility of HarmalaHCl in cold water. By definition, it is directly related to the
HarmalaHCl(↓↓) <--> [HarmalaH+] + [Cl-] equilibrium constant:
K = s^2. For manske purposes, a mixture of two saturated harmalaHCl salts (e.g. harmine and harmaline) behave as a single harmala with solubility
s(Mixture)^2 = s(Harmaline)^2 + s(Harmaline)^2.
r : Harmala recovery ratio after precipitation.
From these definitions, when precipitation is complete,
rh of [harmalaH+] and [Cl-] will have precipitated as HarmalaHCl, leaving
h-rh of [harmalaH+] and
c-rh of [Cl-] in solution. The equilibrium equation for harmalaHCl(↓↓) <--> [harmalaH+] + [Cl-] is therefore:
 Eq. 1
Eq. 1An important first observation in this equation is that when r = 0 (no recovery), hc = s^2. That is, precipitation will not happen until hc > s^2, quantifying part of bullet point a). Eq 1. can be re-arranged to express r as a function of c, h, and s:
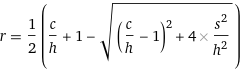 Eq. 2
Eq. 2For example, for h=0.07M and s=0.05M, the expected recovery r can be plotted against c:
 Fig. 1: Harmala recovery rate change with NaCl added. In this example h=0.07M, s=0.05M. The purple line at r=98% recovery corresponds to c ~ 1.85M (equivalent to ~10.8% NaCl).
Fig. 1: Harmala recovery rate change with NaCl added. In this example h=0.07M, s=0.05M. The purple line at r=98% recovery corresponds to c ~ 1.85M (equivalent to ~10.8% NaCl). One question that comes up is, "How much salt do I need to add?" Eq. 1 can also be re-arranged as:
 Eq. 3
Eq. 3The salt needed can be plotted as a function of h (for example, for r = 0.98 and s = 0.05M),
 Fig. 2: [Cl-] needed to achieve 98% recovery rate as a function of [HarmalaH+] (s = 0.05 was assumed for illustration purposes). The minimum [Cl-] point is at h0 = 0.36M and c0 =0.70M (equivalent to 4.09% NaCl). The minimum ionic strength point is also shown (see text).
Fig. 2: [Cl-] needed to achieve 98% recovery rate as a function of [HarmalaH+] (s = 0.05 was assumed for illustration purposes). The minimum [Cl-] point is at h0 = 0.36M and c0 =0.70M (equivalent to 4.09% NaCl). The minimum ionic strength point is also shown (see text).The minimum represents the manske setup where 98% recovery can be achieved with the lowest Cl- concentration. This important point is given by,
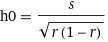
 Eq. 4: The minimum added salt point.
Eq. 4: The minimum added salt point.In our last plot (s = 0.05M, r=0.98 ), the minimum salt point is at h0 = 0.36M and c0 =0.70M (4.09% NaCl). Compared to the other examples, if 6g of FB harmalas are dissolved in 78ml (instead of 400ml), the added NaCl salt concentration can go down by a factor of ~2.6 (from 10.8% to 4.01%) and the same ammount of harmalas will be recovered.
Since excess water helps remove unwanted plant material, harmala dilution away from the lowest salt concentration point could be useful. Let's call the dilution factor 𝛼,
 Eq. 5
Eq. 5The salt concentration to keep the same recovery rate increases to,
 Eq. 6
Eq. 6In our ongoing examples, h = 0.07 was 𝛼 ~ 5x dilution from the minimum salt point (h0=0.36M). Consequently, the NaCl salt concentration was ~ 1/2*(5+1/5) ~ 2.6 higher.
Issues can arise if h is too dilute (large 𝛼

, as the required c will not be reachable.
These examples are only quantitative until s is actually measured/known. I think there are a few conclusions we can make though,
1) The ammount of salt needed is highly dependent on the starting harmala concentration.
2) There is a starting harmala concentration that minimizes the NaCl concentration needed.
3) In practice, diluting the harmalas below the minimum NaCl salt point may be desired to remove excess plant material with the help of additional water, but the NaCl salt concentration will need to increase.
4) By knowing the HarmamaHCl solubility in cold water (s), all these quantities can be calculated and set up. For a desired r:
4.1) Calculate the minimum salt point (h0, c0) using Eq. 4. If excess water is not needed perform the manske there.
4.2) If more water is desired, decide on a dilution factor 𝛼 which will determine a new h and c using Eq. 5-6.
There is a special dilution value that minimizes the combined ionic strength h+c. It can be shown a minimum occurs for h+c when 𝛼 = √(1 + 1/r). In Fig 2. that corresponds to where the slope of the curve is -1, which occurs at h = 0.25M, c = 0.75M.
Note: Heavily edited on 12/1/2020. Images are linked to chat, also adding them here in case they are lost during a hard chat reset.
Loveall attached the following image(s):

0001.gif
(2kb) downloaded 200 time(s).
manske05.gif
(2kb) downloaded 197 time(s).
manske04.gif
(1kb) downloaded 196 time(s).
manske03.gif
(1kb) downloaded 195 time(s).
manske02.gif
(2kb) downloaded 195 time(s).
MSP66411ec281c32859cgae00001bhf1gabc2fgdceh.gif
(3kb) downloaded 185 time(s).
manske09_20201202212854683.jpg
(15kb) downloaded 154 time(s).
manske07_20201201173106988_20201204213243293.jpg
(22kb) downloaded 116 time(s).